Таблично-аналитическая модель полевого транзистора для криогенных температур

Аннотация

В.Н. Бирюков, А.М. Пилипенко, И.В. Семерник

Предлагается модель полевого транзистора, совмещающая достоинства табличных и аналитических моделей. Показано, что вольт-амперную характеристику транзистора можно рассчитать как произведение тока, рассчитанного с помощью простой аналитической модели, и поправочной функции управляющих напряжений на основе двумерного степенного ряда.

Ключевые слова: МОП-транзистор, параметры МОП-транзистора, криогенные температуры, параметрическая идентификация

05.13.18 - Математическое моделирование, численные методы и комплексы программ

05.27.01 - Твердотельная электроника, радиоэлектронные компоненты, микро- и наноэлектроника на квантовых эффектах

Введение
Особенностью полевых транзисторов с изолированным затвором (ПТИЗ), использующихся в глубокоохлаждаемых фотоприемных устройствах, является относительно большая длина канала, что обусловлено необходимостью максимального снижения уровня собственных низкочастотных шумов. Разработка же моделей полевых транзисторов для электронных симуляторов интегральных схем определяется, вследствие непрерывного снижения размеров элементов, необходимостью повышения точности моделирования, прежде всего, короткоканальных транзисторов. К сожалению, высокая точность моделей короткококанальных транзисторов отнюдь не гарантирует высокой точности моделирования длинноканальных [1]. Кроме того, высокая точность современных аналитических моделей ПТИЗ получена, как правило, за счет введения новых параметров, что порождает сложную проблему их идентификации. По этой причине зачастую приходится учитывать, что фактическая точность сложной аналитической модели на практике не достигает ее потенциальной точности [1]. Основное достоинство аналитических моделей – их «физичность» – связь их параметров с конструкторско-технологическими, недостаток – вычислительная сложность, влияющая на время анализа цепей.
Противоречие между точностью и сложностью модели частично или полностью снимется при использовании табличных моделей [2]. Основной проблемой использования табличной модели является интерпретация исходных данных, которые в простейшем случае представляют собой таблицу ,  измеренных значений тока канала и напряжений стока и затвора соответственно. При формальной аппроксимации результатов измерений сплайнами не удается получить неосциллирующие первые производные тока ПТИЗ. Интерполяция сглаживающим сплайном высокого порядка дает удовлетворительные результаты [2], но, естественно, за счет точности и времени моделирования. Основным недостатком табличных моделей является их формальный характер, не позволяющий, например, анализировать цепь в температурном диапазоне тем же способом, которым позволяют сделать это аналитические модели. Далее рассматривается возможность разработки гибридной модели, позволяющей найти компромисс между требованиями физичности, точности, сложности и возможности точного и быстрого определения параметров.

Описание моделей

Решение алгебраического или дифференциального уравнения  f (x), в случае, если известно его грубое приближенное решение  g(x), удобно представить в виде  f (x) = g (x)∙(1 + а ₁ x ¹ + а ₂ x ² + … ), где второй сомножитель оказывается быстросходящимся степенным рядом. Такое решение иногда удается получить, даже если само решение  f (x) в степенной ряд не разлагается.
Можно предположить, что, аналогично, если результат интерполяции вольт-амперной характеристики (ВАХ) ПТИЗ представить в виде , где  – грубая аналитическая модель транзистора, а  – двумерная поправочная функция, аппроксимирующая поправку двумерным (в простейшем случае) степенным рядом, то требования, предъявляемые к поправке, могут оказаться намного слабее, чем к сплайну, аппроксимирующему исходную таблицу . Отметим, что в виде степенного ряда представляется не сама ВАХ прибора, что недопустимо [3], а только поправка к ней, имеющая весьма ограниченную вариацию, которая определяется точностью аналитической модели. Применение поправки в виде степенного ряда на практике позволяет уточнить не только моделируемую функцию, но и ее производные, при условии быстрой сходимости ряда: 1 >> а ₁ >> а ₂ … . Обычно при использовании указанного приема удается ограничиться членами ряда третьего порядка [4].
В качестве аналитической (С∞-непрерывной) далее использовалась модель, предложенная в [5]:
,    (1)
где β, V₀, λ, k – параметры модели;   – оценка напряжения насыщения; мВ – формальная константа, определяющая протяженность промежуточного участка ВАХ между крутой и пологой областями;  – формальная константа, служащая для компенсации погрешности используемого приближенного выражения для напряжения насыщения;.
Все параметры модели (1) являются физическими: β – удельная крутизна; V0– пороговое напряжение; λ – коэффициент, учитывающий конечное выходное сопротивление транзистора на пологом участке ВАХ; k– коэффициент, учитывающий ограничение дрейфовой скорости носителей заряда продольным электрическим полем.
Очевидно, что модель (1) может быть преобразована в таблично-аналитическую следующим образом:
.   (2)
Как было указано выше, поправочная функция  представляет собой двумерный степенной полином. В качестве примера ниже приведены поправочные функции в виде двумерных степенных полиномов второго и третьего порядка соответственно


Алгоритм параметрической идентификации
Идентификация параметров модели (1) производилась методом наименьших квадратов при использовании стандартной программы спуска методом Левенберга–Марквардта. В качестве целевой функции использовалась сумма квадратов относительных погрешностей моделирования тока
.
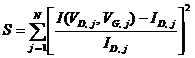Поскольку модель (1) является региональной, то идентификация ее параметров производилась дважды: вначале параметры модели определялись на пологом участке ВАХ, затем при найденном параметре l остальные параметры уточнялись во всей области определения тока.
Для ускорения спуска и повышения точности результатов идентификации в данной работе была проведена редукция размерности задачи минимизации, также как в работах [6] и [7]. Исходная четырехмерная целевая функция S(β, V₀, λ, k) преобразовывалась в двумерную функцию S(V0, k), которая далее оптимизировалась численно. Поскольку параметры β и λ входят в модель (1) линейно, то при использовании необходимых условий минимума  и  можно получить аналитические выражения β = β(V₀, k) и l = l(V₀, k) и преобразовать четырехмерную функцию S(β, V₀, λ, k) в двумерную функцию S(V₀, k).
Определение коэффициентов двумерной поправочной функции , также удобно проводить методом наименьших квадратов. В качестве целевой функции в данном случае можно использовать сумму квадратов отклонений поправочной функции от отношения экспериментальных значений тока к значениям тока, рассчитанным с помощью модели (1)
.
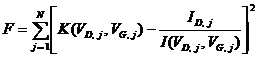Коэффициенты поправочной функции определяются из системы линейных алгебраических уравнений, которую можно получить исходя из необходимых условий минимума целевой функции F
, , , …
Результаты моделирования
Для доказательства эффективности предлагаемой таблично-аналитической модели была проведена идентификация параметров моделей (1) и (2) для тестового образца p-канального ПТИЗ. Длина канала тестового ПТИЗ приблизительно равна 5 мкм. ВАХ транзистора измерялась при температуре T = 4,3 К.
На рис. 1, а приведены экспериментальная выходная ВАХ тестового ПТИЗ и ВАХ, рассчитанные с помощью моделей (1) и (2). Экспериментальная ВАХ показана кружками, результаты расчета, полученные для модели (1), показаны штриховыми линиями. Результаты расчета, полученные для модели (2) при использовании поправочной функции в виде двумерного степенного полинома третьего порядка, показаны сплошными линиями. Поправочная функция в виде двумерного степенного полинома  в трехмерном пространстве представляет собой поверхность, которая показана на рис. 1, б. Точками на этом же рисунке показаны отношения экспериментальных значений тока к значениям тока, рассчитанным с помощью модели (1) .

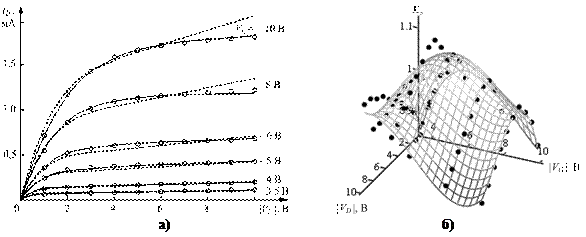
Рис. 1. – Выходные ВАХ тестового ПТИЗ (а) и поправочная функция K₃ (V_D, V_G) (б)

Как видно из рис. 1, б погрешность моделей (1) и (2) в выбранном диапазоне токов и напряжений невелика: . Количественная оценка погрешности моделей и соответствующие им параметры приведены в таблице № 1. Среднеквадратическая относительная погрешность модели  не может однозначно характеризовать точность моделирования, поэтому кроме нее рассчитывалась и максимальная по модулю относительная погрешность │δ│max.
Таблица № 1
Параметры и погрешности моделей ПТИЗ

Из рис. 1 и таблицы № 1 следует, что применение поправочной функции в виде двумерного степенного ряда позволяет значительно повысить точность моделирования ВАХ ПТИЗ для криогенных температур. Так, при умножении аналитической модели на степенной ряд второго порядка, среднеквадратическая и максимальная относительные погрешности полученной модели уменьшаются примерно в 2 раза по сравнению с теми же погрешностями исходной модели. При использовании степенного ряда третьего порядка погрешности модели (2) уменьшаются примерно в 4 раза относительно погрешностей аналитической модели.
Очевидно, что при увеличении порядка поправочной функции, точность таблично-аналитической модели (2) будет возрастать. Особый интерес представляет характер зависимости погрешностей моделирования от порядка поправочной функции m. На рис. 2 приведены зависимости относительной среднеквадратической погрешности и максимальной по модулю относительной погрешности модели (2) от m.

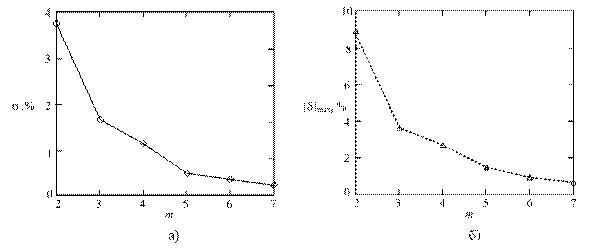
Рис. 2. – Зависимости σ и │δ│max модели (2) от порядка поправочной функции

Как видно из рис. 2 зависимости σ(m) и │δ│max(m) имеют примерно одинаковый характер, причем, чем больше m, тем медленнее уменьшаются обе погрешности. Результаты, представленные на рис. 2, имеют практическую ценность – они позволяют оценить порядок поправочного полинома при заданных погрешностях моделирования. Например, для того чтобы обеспечить условие │δ│max ≤ 1 %, необходимо использовать поправочную функцию как минимум 6-го порядка.
Выводы
Предложенная в данной работе модель (2) относится к классу гибридных таблично-аналитических моделей [8], отличаясь от них лишь тем, что в качестве шаблона предлагается использовать не формальную, а физическую аналитическую модель, параметры которой можно гарантированно определить путем измерений. Таким образом, выбор аналитической модели обусловлен компромиссом между вычислительной сложностью, точностью и легкостью экстракции ее параметров.
Таблично-аналитическая модель не теряет С_∞-непрерывности исходной аналитической модели, то есть не накладывает ограничений на порядок точности численных методов анализа электронной цепи. Вычислительная сложность модели (2), по крайней мере, не превышает вычислительную сложность простейших табличных моделей. Кроме того, модель (2) не более сложно, чем табличные модели, позволяет определять ток вне диапазона таблицы , то есть экстраполировать результаты в нерабочую область ВАХ (последнее необходимо при использовании итераций при численном решении уравнений цепи).
В заключение отметим, что предложенная гибридная модель в определенной степени обладает свойствами используемой аналитической модели. Например, она позволяет анализировать температурный дрейф параметров моделируемых цепей по известным зависимостям параметров ПТИЗ от температуры [9].
Работа выполнена при поддержке стипендии Президента Российской Федерации молодым ученым и аспирантам, осуществляющим перспективные научные исследования по приоритетным направлениям модернизации российской экономики (СП-398.2012.5).

Литература

1. Tsividis Y.P., Suyama K. MOSFET modeling for analog circuit CAD: Problems and prospects [Text] // IEEE Journal of Solid-State Circuits, 1994. – V. 34. – № 3. – P. 210–216.
2. Денисенко В.В. Компактные модели МОП-транзисторов для в микро- и наноэлектронике [Текст]. – М.: ФИЗМАТЛИТ, 2010. – 408 с.
3. McAndrew C.C. Practical modeling for circuit simulation [Text] // IEEE Journal of Solid-State Circuits, 1998. – V. 34. – № 3. – P. 439–448.
4. Бирюков В.Н. Диагностика моделей барьерной емкости диода [Текст] //Радиотехника и Электроника, 2009. – Т. 54. – № 9. – С. 1144–1148. 
5. Бирюков В.Н. Четырехпараметрическая компактная модель полевого транзистора с коротким каналом [Текст] // Нанотехнологии-2010. Тр. международной научно-технической конференции. Ч. 2. – Таганрог: Изд-во ТТИ ЮФУ, 2010. – С. 114–115
6. Бирюков В.Н., Пилипенко А.М. Диагностика статических моделей диода [Текст] // Радиотехника и Электроника, 2009. – Т. 54. – № 5. – С. 604–610.
7. Бирюков В.Н., Пилипенко А.М. Исследование трехпараметрической модели высокочастотного полевого транзистора [Текст] // Изв. вузов. Электроника, 2003. – № 6. – С. 22–26.
8. Bourenkov V., McCarthy K.G., Mathewson A. A. A Hybrid Table/Analytical Approach to MOSFET modeling [Text] // Proceedings of International Conference on Microelectronic Test Structures. – Monterey, CA, 2003. – P. 142–147.
9. Пилипенко А.М., Бирюков В.Н., Исследование параметров полевых транзисторов с изолированным затвором при низких температурах [Текст] // Успехи современной радиоэлектроники, 2011. – № 9. – С. 66–70.