Математическое моделирование процессов в водохранилище на реке Эшкакон и ее практическая значимость
Аннотация
Выведена математическая модель водохранилища. Рассчитана скорость осаждения частиц в водохранилище. Сделан вывод, что водохранилище является предварительным отстойником.
Ключевые слова: водохранилище, предварительный отстойник, математическая модель, скорость осаждения
05.23.04 - Водоснабжение, канализация, строительные системы охраны водных ресурсов
Математические модели все более прочно входят в практику исследований и проектирования систем водоснабжения. Универсальность абстрактного языка математики позволяет обобщать экспериментальные результаты, дает возможность широкого обзора вариантов, как самих систем, так и их технологических режимов эксплуатации, что в свою очередь позволяет отобрать наиболее оптимальные варианты технологических схем комплексов [1,2].
Техника построения модели в области водоочистки зачастую составляет своего рода искусство, доступное разве что математику. Более подробный анализ сущности формализации процесса дает количественные закономерности процесса в блоке. Это означает, что для заданных входных условий блока, используя формализацию процесса, всегда можно найти его результат на выходе. Очевидно, мы имеем дело с предсказанием результата процесса в блоке по входным условиям и формальному представлению процесса. Математическая модель позволяет прогнозировать работу блока [3,4].
При прогнозировании с помощью модели, нельзя сказать о самом процессе, ведь формализация предполагает абстрагирование от внутреннего смысла процесса. Жертвуя пониманием сущности процесса, приобретаем возможность предсказывать его результат. Такой подход является типично прагматическим, то, несомненно, устраивает как эксплуатационника, так и химика-технолога.
В случае зависимости от времени входных условий, которые называются внешним воздействием или просто воздействием на блок, для заданной формализации процесса в блоке можно прогнозировать его результат на любой момент времени. Такой мгновенный результат воздействия называют откликом блока на воздействие.
Процессом в блоке можно управлять, изменяя параметры формализации, определенным образом дозируя реагент, как-то воздействуя на гидродинамику потока. Такое управление отличается от воздействия своей целенаправленностью.
Управляемая технология оптимальна не только по параметрам отклика, но и позволяет сэкономить реагенты, в какой-то мере упрощает обслуживание комплекса, но самое главное гарантирует высокую надежность эксплуатации.
Рассмотрим математическую модель водохранилища как предварительного отстойника, в котором происходит перемешивание потока воды [5]:
| Свых = Свх (1+u/v)-1 |
где u – скорость осаждения; v – скорость транспортного потока.
Эффект отстойника с такой моделью равен:
| K=(1+u/v)-1 |
Потери воды в водохранилище-отстойнике незначительны, т.е.:
| Т=Т1 =Т2 +V/Q |
Эффект реактора смешения равен:
| К=(l+RT)-1 | |
| RT=u/v |
Откуда:
| R=u/vT=uQ/vV=uS/V=uh |
где V – объём отстойника; S- площадь поперечного сечения блока; h- длина в направлении V.
Процесс осаждения в блоке происходит с кинетикой первого порядка:
| Свых =-гСвх/р |
После интегрирования распределение концентрации по высоте со временем, характерное для седиментации по классической теории Эйнштейна-Самолуховского, будет иметь вид:
∫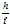 Свыхdh= - ∫ Свыхdh= - ∫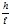 ( иСвхdh) / h ( иСвхdh) / h |
|
| Свых = -uСвхln |h| |
Под h понимается координата точки, отсчитанная от некоторого уровня воды. Кинетическая запись процесса дает распределение скорости осаждения, а ее интеграл - распределение концентрации по высоте на любой момент времени.
В таблице 1 представлены расчёты по математической модели Эшкаконского водохранилища как предварительного отстойника, в створе сечения 1-1, близко расположенному к водозаборному сооружению [6].
Таблица 1
Расчеты по математической модели Эшкаконского водохранилища
|
№ п/п |
Н,м |
Свх мг/л |
Свых мг/л |
V,
мм/с
|
ln |h| |
| 1 | 2 | 3 | 4 | 5 | 6 |
| В межень | |||||
| 1 | 2 | 150 | 1 | 0,0096 | 0,6931 |
| 2 | 10 | 150 | 2,5 | 0,0078 | 2,3 |
| 3 | 20 | 150 | 5 | 0,011 | 2,996 |
| 4 | 24 | 150 | 10 | 0,021 | 3,178 |
| 5 | 32 | 150 | 30 | 0,058 | 3,466 |
|
6 7 |
40 | 150 | 50 | 0,09 | 3,689 |
| 7 | 47 | 150 | 100 | 0,173 | 3,85 |
| 8 | SO | 150 | 150 | 0,253 | 3,912 |
| В паводок | |||||
| 1 | 2 | 1500 | 50 | 0,048 | 0,6931 |
| 2 | 10 | 1500 | 100 | 0,035 | 2,3 |
| 3 | 15 | 1500 | 200 | 0,049 | 2,7 |
| 4 | 20 | 1500 | 300 | 0,067 | 2,996 |
| 5 | 30 | 1500 | 500 | 0,098 | 3,4 |
| 6 | 44 | 1500 | 1000 | 0,176 | 3,784 |
| 7 | 48 | 1500 | 1500 | 0,258 | 3,871 |
Полученные расчеты скорости осаждения по математической модели практически не отличаются от лабораторных исследований.
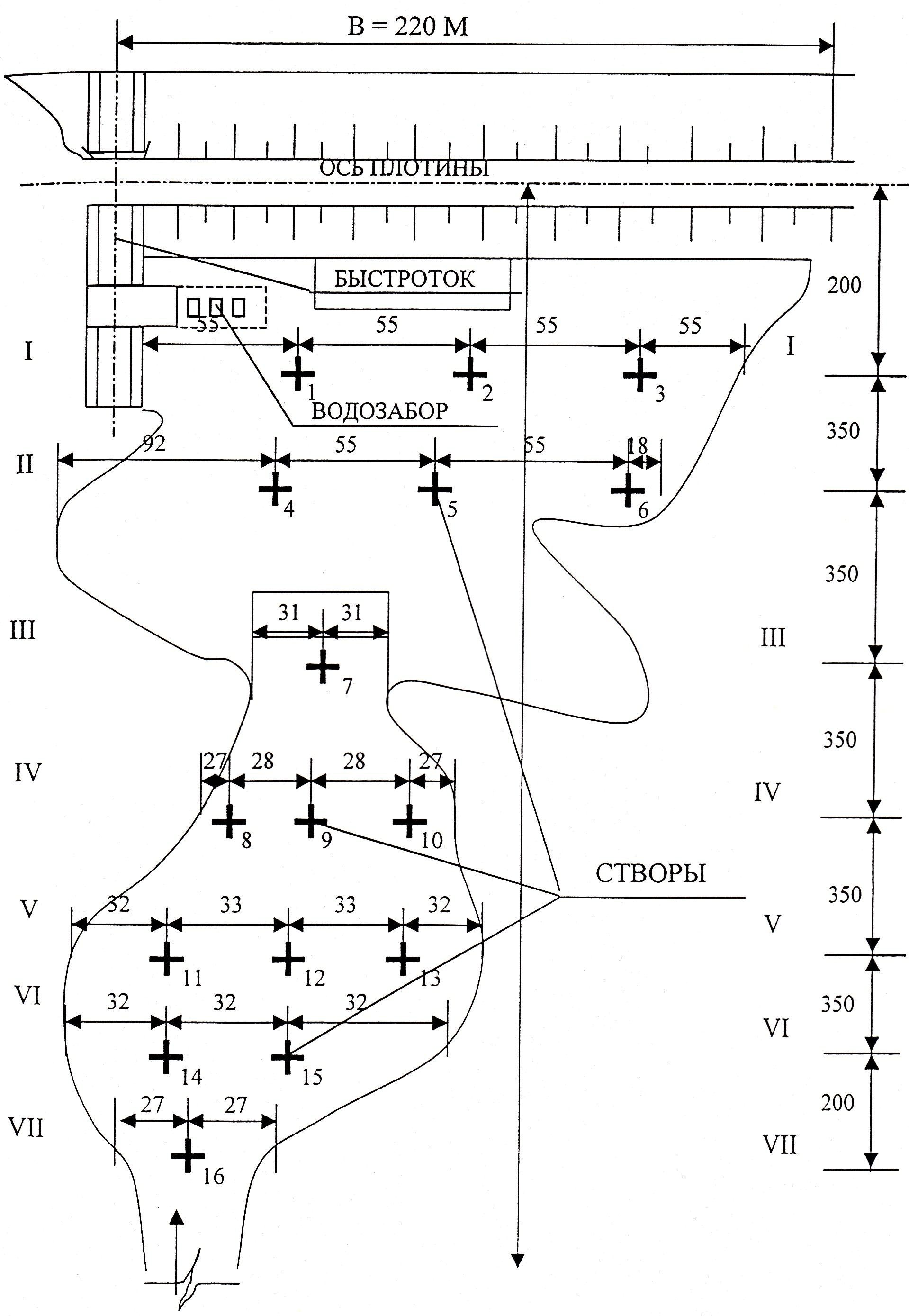
Рисунок 1 Створы на поверхности водохранилища для отбора и исследований проб воды и осадка.
I – VII – поперечные сечения водохранилища;
1 – 16 – номера отбора проб по створам.
Выводы :
-
Проведенные эксперименты регулируемого Эшкаконского водохранилища показали, что оно является огромным предварительным отстойником, в котором происходит очистка воды перед водозаборным сооружением;
-
При многолетних исследованиях выяснилось, что качество воды в водохранилище по всем показателям практически соответствует СанПиНу и обработка её в течение 7-8 месяцев возможна без применения реагентов;
-
Исходя из п.2 выводов, предварительно очищенную воду водохранилища можно подавать для окончательной очистки непосредственно на скорые фильтры с последующим обеззараживанием и подачей потребителю.
Список литературы:
-
Будлей В.Р. Моделирование гидромелиоративных систем. - Киев.: Наукова Дума, 1975, 195 с.
-
А.А.Смоляниченко, А.В.Тихонов, П.Н.Науменко, Н.С.Серпокрылов. Исследование массообменных характеристик аэроторов REHAU RAUBIOXON. Материалы междунарожной научно-практической конференции «Строительство-2012». Ростов-на-Дону.: РГСУ, 2012
-
Н.С.Серпокрылов, Н.Н.Куля. Моделирование линий токов с помощью программного оборудования ANSYS 11. Материалы междунарожной научно-практической конференции «Строительство-2012». Ростов-на-Дону.: РГСУ, 2012
-
Железняков Г.В., Данилевич Б.Б. Точность гидрологических измерений и расчетов. Л.: Гидрометеоиздат, 1966, 115 с.
-
Математические модели контроля загрязнения воды./ Под ред. Джеймса А. – М.: Мир, 1981, 483 с
-
Алешин В.С. Очистка природной низкотемпературной воды. Ростов-на-Дону.: Ростиздат, 2005, 250 с.