Метод определения температуры в произвольной точке здания в условиях неполного охвата сенсорными сетями
Аннотация
В статье рассматривается задача идентификации теплодинамики систем на базе сенсорных сетей, таких как произвольное здание. Дается ее проблематика: рассматриваются слабые места современных интеллектуальных систем на базе сенсорных сетей, существенно ограничивающие их потенциал и повышающие вычислительные затраты. Дается описание нового подхода к построению интеллектуальных автоматических систем управления на базе сенсорных сетей, основанного на методах нечеткого моделирования. Особенность подхода заключается в сохранении высоких показателей эффективности моделирования с уменьшением количества узлов сенсорной системы. В качестве примера реализации методики, рассматриваются результаты анализа экспериментальной имитационной модели термодинамики тестового пространства. Показаны преимущества полученного решения по отношению к существующими коммерческими решениями данной задачи. Проведены испытания методики и показана ее эффективность.
Ключевые слова: интеллектуальные системы управления, сенсорная сеть, анализ данных, нечеткое моделирование, нечеткая классификация, функция принадлежности.Ключевые слова:
05.13.18 - Математическое моделирование, численные методы и комплексы программ
Введение
В последние несколько лет возрос интерес к разработке и изучению беспроводных самоорганизующихся сенсорных сетей (БСС) - сетей, состоящих из множества простых миниатюрных устройств (узлов), каждое из которых содержит микроконтроллер, приемопередатчик и автономный источник питания. Узлы оснащаются сенсорами, способными регистрировать информацию о параметрах физических полей различной природы в местах их расположения. Результаты измерений передаются по многозвенной цепочке (от узла к узлу) в вычислительный центр для обработки и анализа.
В настоящее время БСС находят все более широкое применение в качестве распределенных систем мониторинга различных объектов и физических процессов. Специфика данной задачи определяет общую структуру беспроводных сенсорных сетей, которые, как правило, представляют собой распределенные на большой территории информационно-измерительные комплексы.
В типичной беспроводной сенсорной сети данные, собираемые всеми узлами, хранятся на единственном сервере, выступающем в качестве шлюза с сетью IP. Чтобы достичь шлюза, данные перемещаются по сети от узла к узлу, при этом существует вероятность потери некоторого количества данных, возрастающая с увеличением размера сети. Кроме того, когда узел передает данные соседнему узлу, а тот передает их дальше, расходуется энергия. Сети большого объема с множеством узлов расходуют для передачи данных значительно больше электроэнергии[7].
Отсюда имеем важное ограничение при построении моделей идентификации систем, связанное с ограниченным отражением реальной системы на модель:
- по мере роста сенсорной сети ее производительность снижается
- размерность сети прямо пропорциональна энергопотреблению.
На примере решаемой задачи предлагается метод уменьшения недетерминированности сенсорной системы, используя ее стохастические свойства, с целью максимального отображения реальной системы.
Далее будут рассмотрены методы оптимального проектирования БССи построения на её основе оптимально детерминированной модели, решающей задачу определения значений температур.
Постановка задачи
Первичная постановка задачи. Пусть в трехмерном евклидовом пространстве существует некоторое замкнутое множество гиперплоскостей![]() , образующих ограниченную с
, образующих ограниченную с ![]() сторон область
сторон область![]() Есть замкнутое множество значений некоторой характеристической величины
Есть замкнутое множество значений некоторой характеристической величины![]() , определяющее состояние системы в заданной точечной области определения
, определяющее состояние системы в заданной точечной области определения![]() , непрерывно, нелинейно и, вообще говоря, с некоторой вероятностной мерой распределенное по области
, непрерывно, нелинейно и, вообще говоря, с некоторой вероятностной мерой распределенное по области ![]() . Существует множество сенсорных точек
. Существует множество сенсорных точек ![]() , где для каждой точки
, где для каждой точки ![]() в момент времени
в момент времени ![]() определено значение характеристической величины
определено значение характеристической величины ![]() и с переменной вероятностной мерой, подчиняющейся некоторому закону распределения, определена величина
и с переменной вероятностной мерой, подчиняющейся некоторому закону распределения, определена величина ![]() в пределах некоторой окрестности с центром масс в точке
в пределах некоторой окрестности с центром масс в точке ![]() .
.
-
Требуется идентифицировать оптимальную структуру сенсорной сети, покрывающей область
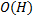 , минимизировав кол-во узлов
, минимизировав кол-во узлов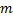 .
. - Требуется определить значение характеристической величины в произвольной точке рассматриваемого пространства.
Конкретизированная постановка задачи. Определив характеристическую величину как температуру системы, параметризованную координатами в рассматриваемом пространстве, а область как анализируемое здание, исходя из условий первичной постановки задачи, необходимо определить значение температуры в произвольной точке здания .
Нечеткая модель как базис для решения задачи определения температур на доверительных интервалах в произвольных точках ограниченного пространства
По определению сенсорная система является детерменированной связанной(сильно или слабо) системой, имеющая контрольные точки, выступающие в роли индикаторов состояния системы.
Тогда можно описать такую систему как вершинный (элементы системы-вершины) граф:
|
|
(1) |
где
|
|
(2) |
- это некоторые неопределенные состояния системы (Q - неизвестно), на заданных параметрах ![]() – координатах области рассмотрения(координата z опущена для упрощения вида расчетов); Q – измеряемая величина, характеризующая состояние системы, в данной задаче - температура.
– координатах области рассмотрения(координата z опущена для упрощения вида расчетов); Q – измеряемая величина, характеризующая состояние системы, в данной задаче - температура.
|
|
(3) |
- это замкнутое множество детерминированных состояний системы на заданных параметрах![]() , что сводится к множеству состояний известных узлов сенсорной сети.
, что сводится к множеству состояний известных узлов сенсорной сети.
|
|
(4) |
- это замкнутое множество связей между локализованными в некоторой точке пространства детерминированными состояниями системы, то есть узлами сенсорной системы. Характер этой связи определяется функцией меры близости узлов сенсорной сети, в соответствии с выбранной метрикой пространства.
|
|
(5) |
где ![]() – число измерения в пространстве,
– число измерения в пространстве, ![]() – множество координат, определяющих положение точки
– множество координат, определяющих положение точки ![]() в выбранном пространстве,
в выбранном пространстве, ![]() - метрика.
- метрика.
Тогда, если система в действительности является детерминированной, то с некоторой мерой адекватности может быть построена нечеткая модель системы.В данном контексте, нечеткая модель, в отличие от стохастической модели, описывает систему как нечеткий граф состояний с нечеткими правилами связей вершин: ![]()
где ![]() - конечное непрерывное множество всех возможных, вообще говоря, определенных с некоторой вероятностной мерой, состояний системы при вариации параметров
- конечное непрерывное множество всех возможных, вообще говоря, определенных с некоторой вероятностной мерой, состояний системы при вариации параметров ![]() внутри их области определения;
внутри их области определения;
![]() – допустимая погрешность или доверительный интервал, такой, что в окрестности
– допустимая погрешность или доверительный интервал, такой, что в окрестности![]() , состояние
, состояние![]() считается достоверно определенным.
считается достоверно определенным.
|
|
(7) |
– нечеткое отношение между множеством![]() и множеством детерминированных состояний элементов системы
и множеством детерминированных состояний элементов системы ![]() на известных параметрах
на известных параметрах ![]() , где
, где ![]() – функция
– функция
принадлежности![]() к
к ![]() (Далее обозначим
(Далее обозначим![]() ). Применительнок сенсорно-сетевым моделям, эту функцию можно определить аналогично (5) как меру близости между векторами параметров системы
). Применительнок сенсорно-сетевым моделям, эту функцию можно определить аналогично (5) как меру близости между векторами параметров системы ![]() при состоянии
при состоянии ![]() и состоянии
и состоянии ![]() .Причем, если имеет место функциональная зависимость
.Причем, если имеет место функциональная зависимость![]() , то
, то ![]() можно интерпретировать как конечный набор нечетких правил отображения
можно интерпретировать как конечный набор нечетких правил отображения ![]() .
.
Введем формулу для оценки погрешности определения состояния:
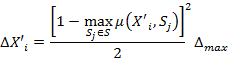 |
(8) |
|
|
(8*) |
где ![]() – некоторая постоянная норма, за которую принимается разница между верхней и нижней границей возможных состояний системы;
– некоторая постоянная норма, за которую принимается разница между верхней и нижней границей возможных состояний системы;![]() –коэффициент точности построенной модели
–коэффициент точности построенной модели ![]() (по сути, среднее значение функции принадлежности
(по сути, среднее значение функции принадлежности ![]() на всей области определения системы ) :
на всей области определения системы ) :![]() (9)
(9)
![]() –вероятность того, что состояние
–вероятность того, что состояние ![]() системы может быть достоверно определено на текущем нечетком отношении
системы может быть достоверно определено на текущем нечетком отношении![]() ; тогда
; тогда ![]() – есть среднее ожидаемое отклонение от реального состояния системы.
– есть среднее ожидаемое отклонение от реального состояния системы.
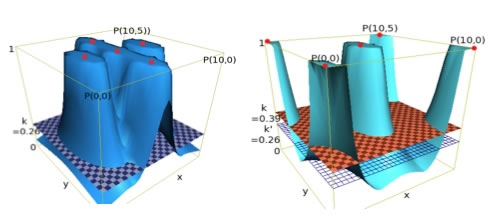
|
а) Менее оптимизированная (число узлов=5) |
б) Более оптимизированная (число узлов=5) |
|
рис. 1 Сравнение нечетких моделей |
|
Следовательно, задача нахождения наиболее адекватной нечеткой модели сводится к максимизации целевой функции (9). Примеры оптимизации нечеткой модели сенсорно сетевой системы без изменения количества узлов иллюстрированы на рис. 1.
Теорема. Для всякого элемента ![]() универсума
универсума ![]() , c оценкой его погрешности
, c оценкой его погрешности ![]() , не выходящей за интервал
, не выходящей за интервал ![]() ,если проекция отношения
,если проекция отношения ![]() на
на ![]()
является нормированным отношением, т.е. функции принадлежности ![]() порождают взаимодополняющие множества
порождают взаимодополняющие множества ![]() , то значение элемента
, то значение элемента ![]()
эквивалентно интегральной сумме всех мер принадлежности ![]() по элементам
по элементам ![]() .
.
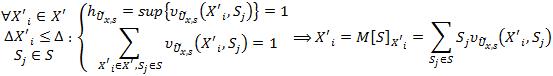 (10)
(10)
Доказательство. Имеем пространство мерой (6), с определенной на нем измеримой функцией![]() , являющейся индикатором измеримого множества
, являющейся индикатором измеримого множества ![]() , а так же являющейся простой, что следует из определения (7). Тогда
, а так же являющейся простой, что следует из определения (7). Тогда ![]() - конечное разбиение
- конечное разбиение ![]() на измеримые множества.
на измеримые множества.
Интегрируя измеримую функцию при ![]() по Лебегу имеем:
по Лебегу имеем:
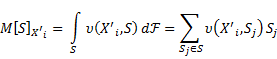 (11)
(11)
Наконец, если рассматривать нормированную функцию принадлежности ![]() как коэффициент подобия, то из условий нормировки
как коэффициент подобия, то из условий нормировки![]() имеем:
имеем: ![]() , что и требовалось доказать.
, что и требовалось доказать.
Замечание.
Если исходное семейство функций принадлежности ![]() не удовлетворяет условию нормировки из (10), то их можно нормировать в соответствии со следующей формулой:
не удовлетворяет условию нормировки из (10), то их можно нормировать в соответствии со следующей формулой:
Заметим, что лишь существование условия нормировки гарантирует закрытие «пропастей» в нечеткой модели.
Методика решения задачи определения температур на доверительных интервалах в произвольных точках ограниченного пространства
Шаг 1. Пространственно-структурная самоорганизация системы.
На этом шаге необходимо определить текущую структуру системы в пространстве: ориентацию узлов и расстояния между узлами, топологию, инициализировать все узлы системы. Использование конкретных алгоритмов зависит от разных факторов системы (наличие перекрытий, акустика и т.д.), выберем лишь наиболее простые.
Для определения ориентации можно использовать алгоритм AoA (см. рис. 2), суть которого заключается в измерении фазы или временного интервала между приемами звукового сигнала на различных узлах [10].
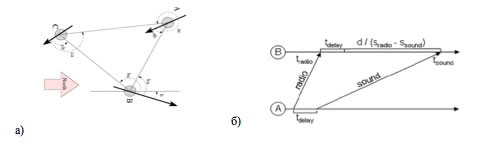
|
|
|
рис. 2 Иллюстрация алгоритма AoA |
Для определения расстояний между узлами можно использовать алгоритм TDoA, суть которого заключается в замере времени прохождения радиосигнала и последовательности звуковых сигналов между всеми парами узлов.
Шаг 2. Инициализация системы.
Определим ![]() из (1), как множество датчиков-индикаторов температуры (
из (1), как множество датчиков-индикаторов температуры (![]() из (1)).
из (1)).
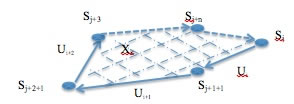
рис. 3 Представление сенсорно-сетевой системы в виде графа
Тогда ![]() из (1) является замкнутым множеством связей графа G. Теперь исходную систему можно представить в виде графа G в соответствии с (1), с параметрами (2), (3), (4) (см. рис. 3).Мерой значимости связей или весом дуг графа G в соответствии с (5) является некоторая функция близости вершин,
из (1) является замкнутым множеством связей графа G. Теперь исходную систему можно представить в виде графа G в соответствии с (1), с параметрами (2), (3), (4) (см. рис. 3).Мерой значимости связей или весом дуг графа G в соответствии с (5) является некоторая функция близости вершин, ![]() -функция. Применительно к сенсорным системам:
-функция. Применительно к сенсорным системам:
|
|
(13) |
Выбор вида функции (6) обусловлен тем фактом, что энергия сигнала, посылаемого одним узлом сети убывает пропорционально квадрату расстояния [9].Таким образом, при значениях ниже некоторого (зависит от технической спецификации сенсоров) ![]() ,
, ![]() выпадает из множества
выпадает из множества ![]() .
.
Шаг 3. Построение нечеткой модели
В соответствии с (6), определим отношение ![]() в виде матрицы смежности.
в виде матрицы смежности.
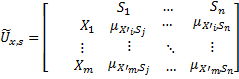
Определим функцию принадлежности из (7)аналогично (5) как некоторую функцию меры пространственной близости:
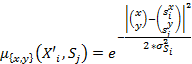 |
(14) |
где ![]() – это некоторая область,
– это некоторая область, ![]() , в которой состояние
, в которой состояние ![]() остается детерминированным (область работы термодатчиков с незначительной погрешностью). Выбор вида функции (14) обусловлен высокой степенью сглаживания и аналогией с функцией нормального распределения вероятности, при которой узел системы с местоположением
остается детерминированным (область работы термодатчиков с незначительной погрешностью). Выбор вида функции (14) обусловлен высокой степенью сглаживания и аналогией с функцией нормального распределения вероятности, при которой узел системы с местоположением ![]() окружен экспоненциально убывающим полем, с градиентом направленным в его же сторону. Благодаря таким свойствам, близкие точки буду обладать большей значимостью своих связей в графе.
окружен экспоненциально убывающим полем, с градиентом направленным в его же сторону. Благодаря таким свойствам, близкие точки буду обладать большей значимостью своих связей в графе.
Проведем операцию нормировки функций принадлежности, воспользовавшись (12).
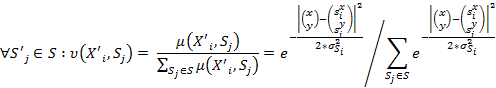 |
(15) |
Как можно заметить, теперь функция ![]() определена на всей области определения
определена на всей области определения ![]() и асимптотически стремится к нулю в направлении всякого вектора
и асимптотически стремится к нулю в направлении всякого вектора ![]() , где
, где ![]() .
.
|
рис. 4 Построение нечеткой модели (4 сенсора, расположенных в углах в комнаты ) |
В итоге имеем следующее семейство поверхностей (см. рис. 4), наглядно демонстрирующих аппроксимирующие свойства полученной нечеткой модели.
Шаг 4.Расчет модели. Все готово для определения состояния моделируемой системы при произвольных её параметрах. А именно, для расчета температуры Q в произвольной точке, воспользуемся теоремой (10):
|
|
(16) |
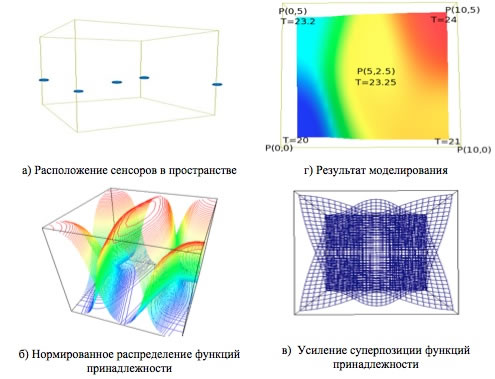
В результате решения исходной задачи имеем поверхность распределения температур в произвольном сечении 3-х мерного пространства (см. рис. 5 (г)).
Экспериментальная апробация метода.
Для испытания метода, в силу недоступности реальных сенсорных систем и их дороговизны для проведения тестов, была разработана программная имитационная модель распределения теплоты в комнате размерами 10 на 5 метров. Схема сенсорной системы идентична рис. 5 (а). Из 5 узлов сенсорной сети, 1 находился в режиме тестера и не включался в модель.
Значения модели для локации узла-тестера сравнивались с показателями самого тестера. Результаты экспериментов представлены в таблице 1.
Таблица 1. Результаты испытания системы.
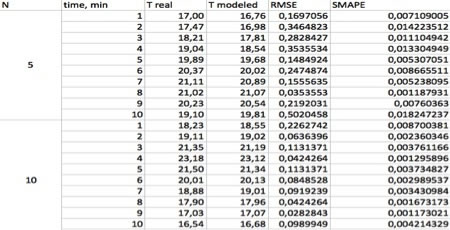
Как видно из результатов, при меньшем кол-во узлов, модель «запаздывает» в определение температуры в искомой точке, в силу того, что изменение показаний далеко расположенных от этой точки сенсоров требует времени. При большем охвате сенсорной сети, это время и отклонения результатов меньше.
Выводы
Предложенная методика эффективно справляется с задачей определения температуры в произвольной точке произвольного подпространства( здания, склада, комнаты) в условиях неполного охвата сенсорными сетями. При сильной нестабильности моделируемой системы в статике(хаотично локализованные сильные перепады температур в пределах рассматриваемого подпространства в случайный момент времени), нечеткая модель будет наименее эффективна, так как её апроксимирующие свойства при неоптимальном охвате сенсорной сетью потеряют влияние на результат (благодаря вводу доверительных интервалов) и конечный результат будет завесить исключительно от меры точности модели(карты локализации и количества узлов сенсорной сети). В случае отсутствия доверительных интервалов, конечные результаты будут маловероятны и, вообще говоря, еще дальше от реальных из-за вносимых погрешностей, на основе неоптимальных апроксимаций. Методика на базе нечеткого моделирования позволит существенно сократить энергозатраты на отопление и охлаждение, в особенности, крупных промышленных объектов, дата-центров, торгово-развлекательных и деловых центров.
Применение методики не ограничивается на решении задачи определения температуры в произвольной точке здания. Методика расширяема и особенно интересна для моделирования динамики систем, в частности таких, как гибридные энергетические системы [7], где определенно может стать алгоритмическим базисом отдельного агента в мультиагентной системе моделирования.
Литература
1.Кофман А. Введение в теорию нечетких множеств — М.: Радио и связь, 1982. — 432 c.
2. Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы - М.: Горячая линия -Телеком, 2006. - 452 c.
3. Brown J. G. - A Note on Fuzzy Sets. Inform, and Control. vol. 18, C. 32-39, 1971.
4. Борисов A. H., Вульф Г. H., Осис Я. Я. Применение теории размытых множеств к идентификации состояния сложных систем. // Кибернетика и диагностика. - 1972. - №5. С. 135-147.
5. Akyildiz I.F., Su W., Sankarasubramaniam Y., Cayirci E., Wireless Sensor Networks: A Survey // IEEE Computer Networks. 2002. vol 38. № 4. С. 393-422.
6. Niculescu D., Nath B. Ad hoc positioning system (APS) using AOA // INFOCOM 2003. Twenty-Second Annual Joint Conference of the IEEE Computer and Communications. IEEE Societies. 2003. vol. 3. №1. С. 1734-1743.
7. Щербаков М.В. Набиуллин А. С. Камаев В.А. Мультиагентная система моделирования производства и потребления электроэнергии в гибридных энергетических системах. // Инженерный вестник Дона. - 2012. - №2. http://www.ivdon.ru/magazine/archive/n2y2012/775/доступ свободный