Кинематический синтез прямолинейно – огибающего механизма щековой дробилки

Аннотация

С. А. Кузнецов, А.В. Владимиров, Ю.В. Белубекова

Представлен кинематический синтез неизвестных параметров исполнительного прямолинейно-огибающего механизма щековой дробилки, которые связаны зависимостями с известными параметрами камеры дробления, разгрузочной и загрузочной щели. Зависимости получены на основе метода интерполяционного приближения функции. Представлено описание щековой дробилки со сложным огибающим движением исполнительного органа, ее достоинства и область применения.
Ключевые слова: прямолинейно-огибающий механизм, кинематический синтез,  щековая дробилка.

Ключевые слова:

05.02.13 - Машины и агрегаты (по отраслям)

Повышение уровня экологической безопасности в сочетании с расширяющимся ассортиментом стеклянных изделий, в частности, стеклотары, требует нового подхода к их утилизации – через предварительное измельчение, которое облегчает транспортировку стеклобоя к потребителю. В странах Евросоюза эта задача решается при помощи компактного дробильного оборудования, которое устанавливается в подсобных помещениях учреждений, торговых центров, гостиниц и т.д. Опыт их эксплуатации позволяет сформулировать комплекс требований, предъявляемый к дробилкам нового поколения: они должны быть компактны, малошумны, безопасны и энергоэффективны.  Кроме того, потребитель измельченного сырья заинтересован в однородности получаемой фракции по размерам осколков.
Перспективным решением в контексте заявленных требований представляется использование в качестве исполнительного механизма щековой дробилки прямолинейно-огибающего механизма на базе кривошипно-кулисного привода [1]. Такой выбор обусловлен двумя факторами:
- незначительными требованиями к точности огибания и
- значительным углом рабочего хода для данной схемы, превышающим 180o
Указанные факторы позволяют применить к данной схеме интерполяционный метод синтеза по трем точкам, что соответствует промежуточному приближению, так как симметричная шатунная кривая кривошипно-кулисного механизма является кривой шестого порядка. В случае промежуточного приближения приравниваются абсциссы направляющей точки М в среднем положении (при φ1=0) и в крайнем положении, соответствующем концу интервала приближения (для кривошипно-ползунного механизма с шатунной кривой четвертого порядка такое приближение соответствует наилучшему) [3].

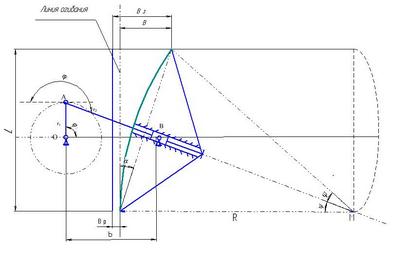
Рис. 1 - Прямолинейно-огибающий механизм щековой дробилки со сложным движением щеки

На рисунке 1 представлен прямолинейно-огибающий механизм щековой дробилки, который характеризуется следующими параметрами рабочего пространства – камеры дробления:  - угол раскрытия рабочего органа, – ширина загрузочной щели,  – ширина разгрузочной щели,  – высота камеры дробления, соответствующая длине интервала приближения.
Кинематический синтез параметров прямолинейно-огибающего механизма дробилки требует определения неизвестных параметров: длины кривошипа , расстояния между точкой сочленения кривошипа и шатуна и направляющей точкой  , длины шатуна , радиуса кривизны дуги , образующего поверхность подвижной щеки и длину дуги  подвижной выпуклой щеки из условия промежуточного приближения при заданных параметрах , , , . [2].
Угол раскрытия рабочего органа  щековой дробилки (рис.1):
, где     (1)
Ширина  загрузочной щели камеры дробления задается от размеров принимаемой на переработку стеклотары (стеклобоя), а ширина  разгрузочной щели соответствует размерам получаемой фракции стеклобоя после переработки.
Условие равенства абсцисс направляющей точки М в середине и конце интервала приближения можно выразить в виде:
;
где    =π - угол поворота кривошипа, соответствующий середине интервала приближения,
=2π - значение функции положения шатунной плоскости в середине интервала приближения при ;
=π/2 - угол поворота кривошипа, соответствующий концу интервала приближения;
=2π-ψ - функция положения шатунной плоскости в конце интервала приближения.                   
С учетом функции положения шатунной плоскости  имеем:
   (2)
Преобразовав уравнение (2) выразим параметр :
.   (3)
Длину прямолинейного участка траектории движения точки М  или высоту камеры дробления можно представить в виде:
,                                              
Поскольку   задается с учетом габаритной высоты устройства и является известным, можно найти  с учетом  и функции поворота шатунной плоскости :
(4)
По теореме синусов из треугольникаOАВ составим соотношение:
,
отсюда длина стойки                    ,    (5)
Движение «огибание» рабочим органом не должно сопровождаться скольжением  между прямой и огибаемой дугой окружности, то есть между выпуклой поверхностью подвижной щеки и прямолинейной поверхностью неподвижной щеки дробилки. Это позволяет избежать возникновения сил трения в пятне контакта, обеспечить стойкость инструмента и одномерность получаемой фракции продуктов дробления. Скольжение равно нулю, если разность между перемещением точки М на расстояние L  и перемещением огибающей дуги длиной l за это же время равна нулю:

где  - длина дуги, образующей поверхность рабочего органа, которая рассчитывается по формуле:
    (6)
Подставив функции для L иl в уравнение (6), определим радиус дуги окружности при условии нулевого суммарного скольжения:
,
отсюда                                     . (7)
Таким образом, решая последовательно уравнения (1),(3),(4),(5),(6),(7), определяем кинематические параметры механизма дробилки, исходя из заданных геометрических размеров камеры дробления щековой дробилки.

Литература

1. 1.А.С. 1646596 СССР, МКИ3 В02С 1/02. Лабораторная щековая дробилка [Текст] / А.Н. Дровников, С.А. Кузнецов, Г.Г Демиденко, Е.Б. Кузнецова. - № 4440074/33 ; заявл. 18.04.88 ; опубл. 07.05.91, Бюл. № 17. – 4 с. : ил.
   2.Кузнецов С.А. Прямолинейно-огибающие механизмы. Анализ и синтез: монография. [Текст] / С.А. Кузнецов, А.В. Владимиров. – Шахты: Изд-во ЮРГУЭС, 2007. – 139 с.