Устойчивость линейных дифференциальных уравнений с постоянным запаздыванием, описывающих процесс фрезерования

Аннотация

А.Я. Красильников, К.Ю. Кравченко

Дата поступления статьи: 06.02.2014

Рассматривается вопрос об устойчивости процесса фрезерования. В статье предложена модель концевого фрезерования с одной степенью подвижности. Предложена функция силы резания для рассматриваемой модели. Составлено соответствующее уравнение движения. Получено унифицированное линейное дифференциальное уравнение с постоянным запаздыванием. Сформулирована теорема об асимптотической устойчивости унифицированного уравнения. Унифицированное уравнение позволяет определять границу устойчивости на плоскости относительных параметров. Предложенный подход позволяет рассмотреть вопрос об устойчивости движения целой группы фрезерных станков с единственным схожим параметром – коэффициентом демпфирования. В работе описан метод оптимизации параметров обработки по критерию асимптотической устойчивости. В результате программной реализации предложенного метода получен график зависимости осевой глубины резания от относительного радиального врезания инструмента в материал заготовки. Сформулирована теорема о существовании экстремума функции зависимости осевой глубины резания от относительного радиального врезания

Ключевые слова: устойчивость, фрезерование, дифференциально-разностные уравнения, колебания, оптимизация

05.02.08 - Технология машиностроения

В ходе изучения процессов механической обработки был обнаружен эффект наложения волн при возникновении автоколебаний [1, 2]. При этом поведение системы описывается дифференциальными уравнениями с запаздывающим аргументом (ДУЗА). Исследование устойчивости ДУЗА позволило построить диаграммы устойчивости на плоскости параметров резания. Графики, отображающие положение кривой границы устойчивости на плоскости «глубина резания – скорость вращения шпинделя», уникальны и однозначно определяются динамическими характеристиками отдельно взятой системы деталь-инструмент-приспособление-станок (ДИПС). В то же время, диаграмма устойчивости позволяет определить оптимальные режимы обработки, обеспечивающие устойчивость резания при высокой скорости снятия материала. В связи с этим вопрос об эффективном быстром построении таких диаграмм является актуальным.
Автоколебания всегда существуют при резании. Традиционно, во избежание неустойчивого режима автоколебаний параметры обработки значительно занижаются. Для проектирования эффективной обработки необходимо оптимизировать режимы резания по критерию асимптотической устойчивости.
В ряде работ, среди которых [3, 4, 5], представлена и исследована на устойчивость одномерная модель фрезерования. При механической обработке, в частности, при фрезеровании на обработанной поверхности остается след от колебаний режущей кромки, вызванных силой резания. При последующем резании этой поверхности режущая кромка режет уже с переменной глубиной резания, зависящей от колебаний предыдущего зуба фрезы. Сила резания при этом, зависящая от глубины резания, также осциллирует.
Ниже представлена схема концевого фрезерования в ортогональной плоскости с одной степенью свободы в случае попутного направления фрезерования (рис.1).

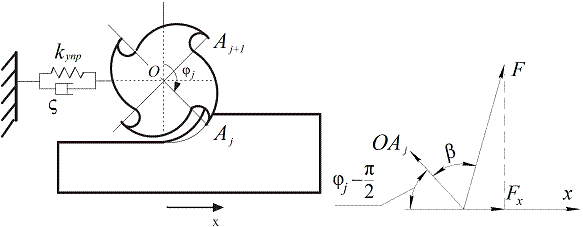
Рис.  1. – Схема фрезерования с одной степенью свободы

Представленная схема позволит описать модель фрезерования с учетом вращения инструмента. Уравнение движения рассматриваемой системы имеет вид 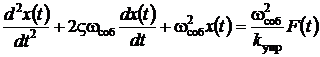(1).
, (1)                  
где ς – относительный коэффициент демпфирования; ω_соб – частота собственных колебаний, рад/с; k_упр – коэффициент упругости, Н/м; Т – постоянный период запаздывания, с; F(t) – сила резания, Н.
Мы рассматриваем систему с одним возможным смещением вдоль оси OX. Величина проекции силы F(t) на выбранную ось определяется 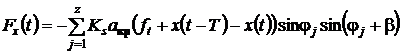(2):
,(2)                
где K_s – удельная сила резания, МПа; a_кр – осевая глубина резания, мм; f_t – подача на зуб, мм/зуб; φ_j – угловое положение j зуба относительно положительной полуоси OY; z – эффективное число зубьев, одновременно участвующих в резании; T – период запаздывания между двумя последовательными резами, Т = 60/(z_обN), где N – скорость шпинделя, об/мин; z_об – общее количество зубьев; β = π/2–γ, где γ – передний угол инструмента.
Постоянное значение K_sa_крf_tsinφ_jsin(φ_j+β) не влияет на устойчивость системы, поэтому его можно отбросить при дальнейшем анализе, исследуя лишь динамическую составляющую силы резания. В проекции на ось OX получим уравнения для компонента F_x 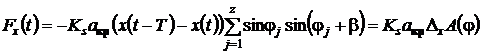(3).
,  (3)   
где Δ_x = x(t–T) – x(t).
Параметр A(φ) изменяется во времени, т.к. φ = φ(t), причем A∈L₂([φ_st, φ_ex]), где φ_st – угол входа фрезы в контакт с заготовкой, φ_ex – угол выхода фрезы из контакта с заготовкой. Перейти к независимому от φ виду возможно путем рассмотрения первого члена соответствующего ряда Фурье 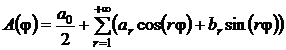(4).
,   (4)                    
где коэффициенты Фурье функции:
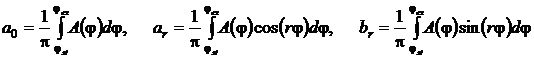(5)
Рассматривая только первый член ряда Фурье мы накладываем ограничение на модель в виде малости периода контакта каждого зуба фрезы с заготовкой. Иными словами, рассматриваем случай, когда радиальная глубина резания составляет всего несколько процентов от диаметра фрезы. Однако, как показано в [6], рассмотрение только первого члена ряда Фурье возможно для всего диапазона значений радиальной глубины резания. Таким образом, переходя к инвариантному во времени виду, получим 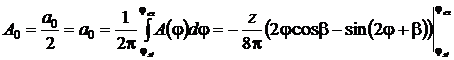(6).
(6)      
В рассматриваемом исходном уравнении (1) произведем следующие замены, согласно 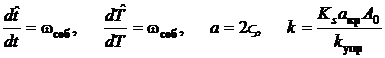(7).
   (7)           
Тогда уравнение (1) примет вид 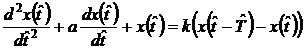(8):
  (8)                  
Уравнение (8) описывает рассматриваемую систему резания с одной степенью свободы в унифицированном виде с безразмерными коэффициентами a и k. Заметим, что коэффициенты a и k являются положительными вещественными числами.
Поставим задачу определить границу устойчивости уравнения (8) на плоскости параметров  и k при фиксированном значении параметра a. Для этого исследуем нулевое состояние равновесия на устойчивость. Критерием асимптотической устойчивости является отрицательность вещественной части всех характеристических показателей дифференциального уравнения. Другими словами, существует такое значение , при котором корни характеристического уравнения на комплексной плоскости переходят из правой полуплоскости в левую полуплоскость и наоборот.
Теорема 1. При фиксированном значении параметра a уравнения (8) каждому значению параметра  соответствует такое значение параметра kкр, что для любых k < kкр решение уравнения асимптотически устойчиво при условии
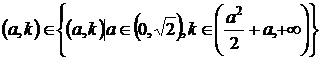   (9)                    
Доказательство. Определим решение соответствующего однородного уравнения как x() = Xexp[iω–]. Тогда x(–) = x()exp[i] согласно [5]. Подставим указанные выражения в уравнение (8).
                                   
где  = ω–ε_Ψ; ε<sub>Ψ – сдвиг между фазой  функции без запаздывания и фазой  функции запаздывания; i – мнимая единица. Результатом решения уравнения (10) относительно ω является (11).
(11)                                   
где ω0 = .
Уравнение (11) при рассмотрении полуоси ω± > 0, а также условие положительности параметров a и k приводит к набору ограничений, который гарантируют дальнейшую структуру области неустойчивости.

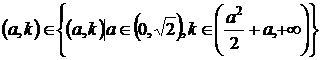
Как показано в [5, 7] исходное уравнение (1) на мнимой оси может иметь корни ±ω+ и ±ω– для всех ω± > 0, исходя из критерия устойчивости Найквиста, при  = 2πL, где L = 0, 1, 2, …  В то же время значение фазового сдвига определяется как (12) согласно [7]. Исходя из вышеизложенного, получим (13).
   (12)                               
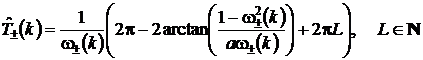     (13)
Критическое значение kкр численно равно минимальному значению k, удовлетворяющему условию (13) для фиксированного значения .
Теорема доказана.
Зависимость (13) является уравнением кривой устойчивости. Ранее [1, 3, 5, 7, 8] кривая устойчивости задавалась параметрически. Очевидно, что граница устойчивости на плоскости параметров  и k состоит из счетного числа подобных элементов (L – натуральное число). Каждый элемент границы будет складываться из двух несимметричных половин – –(k) и –(k). Кривые –(k) и –(k) сближаются, только если –→0, что возможно в единственном случае, когда k → k0, где k0 = a2/2 + a.
Сделаем ряд замечаний. Во-первых, параметры a и k являются безразмерными. Безразмерной величиной, следовательно, также является и относительная частота колебаний ω±. В действительности, значение ω± есть отношение частоты осцилляций к собственной частоте системы ωсоб. Во-вторых, ограничения (9) носят условный характер. Эти ограничения определяют существование вещественных корней на полуоси ω > 0. Как показано, на этой полуоси ω имеет всего два корня – ω+ и ω–. Значение параметра k = k0 задает предел, ниже которого расположена зона устойчивых решений и нет участков неустойчивых решений. Выше предела k = k0 появляются зоны неустойчивости.
Одним из параметров резания является величина относительного радиального врезания RI = b/Dфр, где b – ширина фрезерования, мм; Dфр – диаметр фрезы, мм. Этот параметр характеризует глубину резания в ортогональной плоскости и также влияет на устойчивость обработки. При попутном фрезеровании RI(φΔ) = 0,5(1–cosφΔ), при встречном фрезеровании RI(φΔ) = 0,5(1+cosφΔ), где φΔ = φex – φst.
Теорема 2. Функция aкр(RI) на отрезке RI∈(0,1) имеет хотя бы один экстремум, причем при k=const
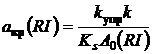    (14)                                   
Доказательство. Исходя из сделанной замены (7), получим 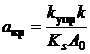(15).
   (15)                                         
Очевидно, что поведение функции aкр(RI) при постоянных прочих параметрах будет зависеть от поведения функции A0(RI). Выразим A0 из (6) через φΔ, причем φex = π для попутного фрезерования и φst = 0 для встречного фрезерования (16).
  (16)                 
где «–» – для случая попутного фрезерования, «+» – для случая встречного фрезерования, φΔ∈(–π, 0)∪(0, π) исходя из RI∈(0,1). Диапазон φΔ ∈(–π, 0) соответствует попутному фрезерования, φΔ ∈(0, π) – встречному, исходя из условия положительности aкр.
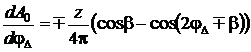(17)                          
Таким образом, функция A0(φΔ) испытывает максимум при φΔ = (–π+β) для попутного фрезерования и максимум при φΔ = β в случае встречного направления фрезерования. Соответствующая функция aкр(RI) достигнет минимума при RI = 0,5(1–cosβ) при попутном фрезеровании и минимума при RI = 0,5(1+cosβ) при встречном фрезеровании.
Теорема доказана.
Сделаем замечание. В формулировке теоремы 2 нет указания на вид экстремума, поскольку вид функции A0(φΔ) зависит от выбранной оси координат, в нашем случае это ось OX. При выборе основной оси OY функция A0(φΔ) также будет иметь экстремумы, но не обязательно максимумы.
С помощью изложенных теорем разработан метод оптимизации режимов резания по критерию асимптотической устойчивости. Ранее метод оптимизации параметров резания был предложен в [9], однако предложенный метод является последовательным. Кратко, метод, изложенный в [9], сводится к последовательности шагов:
1. для произвольного значения RI=1 построить график границы устойчивости aкр(N);
2. на графике задать пару (aкр, N);
3. варьируя RI в пределах от 0 до 1, для выбранного на шаге два значения N определить множество значений aкр;
4. на плоскости aкр(RI) расположить пары (aкр, RI).
Новый метод с параллельной оптимизацией параметров резания сводится к следующей последовательности вычислений:
1. задать пару (k, ), удовлетворяющую условию k < kкр и  = (k), согласно теореме 1;
2а. вычислить N = 60ωсоб/(zоб);
2б. для диапазона RI∈(0,1) вычислить значения aкр при выбранном значении k. 
3. построить график aкр(RI)
Шаги 2а и 2б не являются зависимыми и могут быть выполнены параллельно. Таким образом, оптимизация параметров резания разделяется на оптимизацию скорости шпинделя и оптимизацию пары параметров – осевая глубина резания и относительное радиальное врезание. Также, как следует из (7), изменение жесткости системы влечет изменение параметра aкр, а варьирование частоты собственных колебаний ωсоб влияет на изменение величины скорости вращения шпинделя.
Разделение оптимизируемых параметров в значительной степени упрощает программное решение задачи, поскольку для реализации первого метода требуется перебирать массивы в поисках aкр. В то же время новый метод позволяет работать локально, поскольку изначально задана пара (k, ).
Применение программных методов является неотъемлемым аспектом математического моделирования [10, 11]. Для решения задачи оптимизации применялся язык объектно-ориентированного программирования Python 2.6.
На рис.2 изображена граница устойчивости для группы системы с коэффициентом относительного демпфирования 1,65%.</sub>

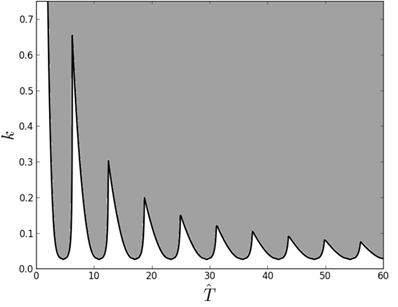
Рис. 2. – Граница устойчивости для a = 0,033 (серым цветом показана область неустойчивых решений)

Соответствующая граница устойчивости для параметров ω_соб = 1308,11 Гц и k_упр = 4,459∙10⁵ Н/м, K_s = 1253 Мпа, β = 61°, z = 1, z_об = 4, φ_st = –π/2, φ_ex = –π приведена на рис. 3.

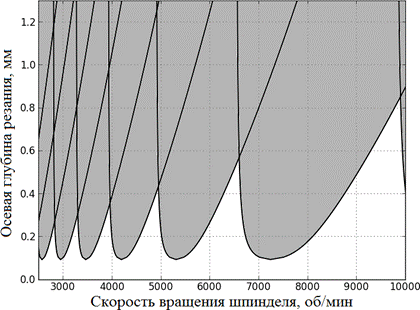
Рис. 3. – Граница устойчивости для a=0,0165, ω_соб = 1308,11 Гц, k_упр = 4,459∙10⁵ Н/м, K_s = 1253 Мпа, β = 61°, z = 1, z_об = 4, φ_st = –π/2, φ_ex = –π

Для скорости шпинделя 9000 об/мин, что соответствует  = 13,7 на рис.4 представлен график зависимости a_кр(RI).

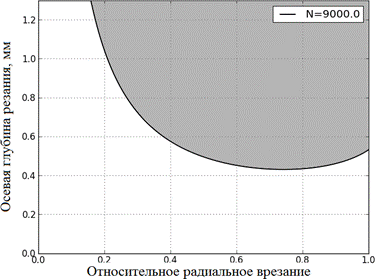
Рис. 4. – График зависимости a_кр(RI) при N = 9000 об/мин

Очевидно, что кривая на рис.4 имеет минимум. По графику можно задать пару (a_кр, RI), соответствующую устойчивому режиму автоколебаний. В результате оптимизации определяются три параметра резания, соответствующие устойчивому режимы автоколебаний.
В статье рассмотрена модель концевого фрезерования с одной степенью подвижности. Составлено соответствующее уравнение движения. Получено унифицированное линейное дифференциально уравнение с постоянным запаздыванием. Сформулирована теорема об асимптотической устойчивости унифицированного уравнения. В работе описан метод оптимизации параметров обработки по критерию асимптотической устойчивости.

Литература:

1. Tobias, S. Machine tool vibration / S. Tobias. – New York: Wiley, 1961. – 352 p.
2. Tlusty J., Polacek M. The stability of the machine tools against self-excited vibrations in machining // International Research in Production Engineering, 1963, 1(1), P. 465-474.
3. Budak E,Altintas Y. Analytical prediction of chatter stability in milling – Part I: general formulation // Journal of Dynamic Systems, Measurement and Control, Transactions of ASME, 1998, 6(1), P. 22-30.
4. Stepan G. Modeling nonlinear regenerative effects in metal cutting // Philosophical transactions of the Royal Society of London, Series A., 2001, 359(1781), P. 739-757.
5. Красильников А.Я., Кравченко К.Ю. Исследование устойчивости систем с запаздыванием, описывающих процесс фрезерования в случае с одной степенью свободы // Вестник машиностроения, 2013. – №9. – С.  67-75.
6. Budak E. Mechanics and dynamics of milling thin walled structures: Ph.D thesis, the University of British Columbia, 1994. ­– 284 p.
7. Красильников А.Я., Кравченко К.Ю. Аналитические методы исследования устойчивости систем с запаздыванием, описывающие процесс фрезерования // Справочник. Инженерный журнал с приложением, 2013. – №9 – С. 23-31.
8. Insperger T., Stepan G., Turi J. State-dependent delay in regenerative turning processes // Nonlinear Dynamics, 2007, 47(1), P. 275-283.
9. Budak E., Tekeli A. Maximizing Chatter Free Material Removal Rate in Milling through Optimal Selection of Axial and Radial Depth of Cut Pairs // CIRP Annals - Manufacturing Technology, 2005, 54(1), P. 353-356.
10. Литвинов С.В., Клименко Е.С., Кулинич И.И. и др. Расчет на устойчивость стержней из ЭДТ-10 при различных вариантах закрепления [Электронный ресурс] // «Инженерный вестник Дона», 2011, №2. – Режим доступа: http://ivdon.ru/magazine/archive/n2y2011/415 – Загл. с экрана. – Яз. рус.
11. Зотова Е.В., Панасюк Л.Н. Численное моделирование динамических систем с большим числом степеней свободы на импульсные воздействия [Электронный ресурс] // «Инженерный вестник Дона», 2012, №3. – Режим доступа: http://ivdon.ru/magazine/archive/n3y2012/933 – Загл. с экрана. – Яз. рус.