О методах измерения малых индуктивностей для радиотехнических систем на кристалле

Аннотация

В.Г. Сапогин, Н.Н. Прокопенко, А.С. Будяков

Дата поступления статьи: 13.03.2013

Обсуждается метод измерения индуктивностей (L) порядка 1 нГн и меньше, заключающийся в проведении двух измерений L: первый раз - на длине шлейфа l0, а второй раз – на длине шлейфа, укороченной в N раз. Получена формула для расчета погрешности неизвестной индуктивности, в которой подбором параметров удается добиться определения L с погрешностью, близкой к погрешности прибора. Показано, что требуемая погрешность измерения начальной длины шлейфа для N=2 и N=5 находится в диапазоне десятков микрометров. Рассмотрены методы ее уменьшения. Сделана оценка базовой длины шлейфа, которая для N=2 и N=5 составляет значения 6,6 мм и 8,3 мм соответственно.

Ключевые слова: индуктивность, метод наименьших квадратов, приборная погрешность, база шлейфа

05.13.05 - Элементы и устройства вычислительной техники и систем управления

Введение. Современные технологии создания IP – модулей и СФ-блоков систем на кристалле используют индуктивности, величины которых лежат в диапазоне от 0,1 нГн до 10 нГн [1-3] и применяются в схемах усилителей мощности [4], в составе активных фильтров СВЧ-диапазона [5-7], пассивных трансформаторов [8], устройствах оптической связи [9] и т.д. Как показано в [10], важнейшим физическим свойством цилиндрических круглых проводников, подводящих к индуктивности ток, является их погонная индуктивность. Проведённые в [10] расчёты указывают на то, что её значение складывается из двух составляющих: индуктивности, которая связана с потоком магнитного поля, возникающего в области протекания тока, и индуктивности, которая связана с магнитным полем, возникающим вне тока.
В связи с этим, полная погонная индуктивность круглого проводника зависит от двух параметров: постоянного значения токовой индуктивности L_c/l=µ₀/4p и безразмерного параметра среза поля ξ₀=r₀/R, где l – длина проводника, r₀ – радиус среза поля, R – радиус проводника, µ₀ – магнитная постоянная.
При изменении параметра ξ₀=r₀/R в интервале от 5 до 100 приведённая полная индуктивность L_f/L_c изменяется в пределах от 4,2 до 10,2. Поскольку этот диапазон совпадает с диапазоном значений индуктивности, используемой в микросхемотехнике, то возникает проблема измерения малых индуктивностей. Она заключается в том, что погонная индуктивность может в несколько раз увеличить измеряемую индуктивность и, тем самым, исказить интерпретацию полученных результатов.
О методах измерения погонной индуктивности и параметра среза магнитного поля. Для более точного измерения погонной индуктивности и параметра среза магнитного поля предлагается следующий метод. К известной индуктивности L₀ подключаются симметрично участки круглого проводника одного диаметра, но с различной длиной l. Первый раз проводник имеет длину l₀, а последний раз длину Nl₀. Где N – число наращивания одинаковых секций. Схема наращивания индуктивности L₀ представлена на рис. 1, где a и b – клеммы подключения измерительного прибора (ИП).

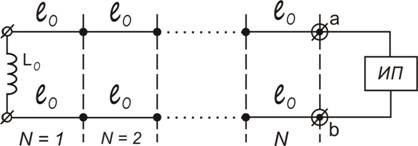
Рис. 1.- Схема наращивания индуктивности L₀

При проведении N наращиваний прибор даст N показаний: L₁, L₂, …, L_N. При первом измерении имеем значение индуктивности
.    (1)
При последнем измерении получим
.   (2)
Зная значения L₀, l₀, можно получить связь для N измеренных значений погонной индуктивности. Значения L_N будут линейно нарастать с увеличением параметра N.
Применим метод наименьших квадратов (линейный регрессионный анализ). В нем линейная зависимость (2) заменяется уравнением
,   (3)
где b₀ и b₁ – постоянные значения лучшей прямой, построенной в облаке экспериментальных точек, которые необходимо найти по методу наименьших квадратов. Значения x пропорциональны длине 2l₀, т.е. эквидистантны. Значение b₀ совпадает с L₀ а значение b₁ будет совпадать с неизвестным значением погонной индуктивности L_п. Тогда связь параметров (3) и (2) имеет вид
,                                       
,     (4)
.                             
Из метода наименьших квадратов следует формула для вычисления среднего значения погонной индуктивности:
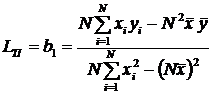,   (5)
где среднее значение , а среднее значение .
Для вычисления погрешности определения погонной индуктивности применяем соотношения:
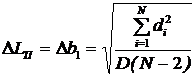,      (6)
где,      (7)
.        (8)
По вычисленным значениям L_П и DL_П можно рассчитать вклад потоковой части в полную погонную индуктивность из соотношения, полученного в [1]
.   (9)
Относительную погрешность этого вклада можно оценить из формулы
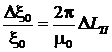.  (10)
Из (10) следует, чем меньше оценка абсолютной погрешности определения погонной индуктивности, тем меньше относительная погрешность определения безразмерного параметра среза поля.
В случае отсутствия индуктивности L₀=b₀=0 (концы l₀ – закорочены) объём вычислений уменьшается, поскольку наилучшая прямая в облаке экспериментальных точек проходит через начало координат. Тогда (5) упрощается и имеет вид
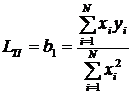,   (11)
При этом формулы вычислений погрешности (6,7,8) остаются прежними.
О методе измерений индуктивности со значением, близким к 1 нГн. При измерениях индуктивностей со значением порядка 1 нГн и меньше можно использовать предлагаемый ниже метод 2-х отсчетов. На рис. 2 показаны схемы измерений, где приняты те же обозначения, что и на рис. 1.

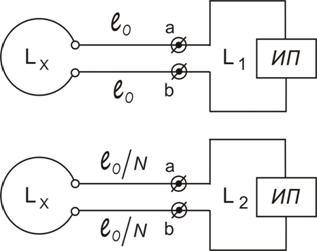
Рис. 2. - Схемы измерений индуктивности

Первый отсчет даёт приборное значение индуктивности L₁
.   (12)
Второй отсчет дает приборное значение индуктивности L₂
,  (13)
где N показывает, во сколько раз была укорочена первоначальная длина шлейфа.
Вычитая из (12) равенство (13), получим для погонной индуктивности
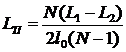,      (14)
а для неизвестной индуктивности
.    (15)
Формула (14) может быть использована самостоятельно для реализации ещё одного метода измерения погонной индуктивности двумя отсчётами. Из неё следует погрешность измерений ΔL_П:
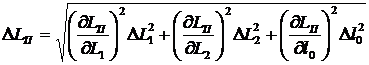.                   (16)
Вычислим частные производные в (16).
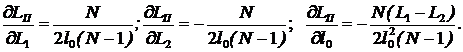           (17)
Подставляя (17) в (16) и принимая во внимание, что приборная погрешность одинакова для двух измерений , а погрешность измерения первоначальной длины шлейфа l₀ можно сделать малой, получим
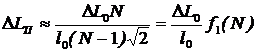.      (18)
Из (18) видно, что погрешность измерения погонной индуктивности можно уменьшать увеличением первоначальной длины шлейфа и коэффициента его укорачивания. В табл. 1 приводятся значения функции f1(N) для разных коэффициентов укорачивания шлейфа N.
Таблица 1
Значения функции f₁(N) для разных коэффициентов укорачивания N

Формула (15) позволяет определить погрешность измерения неизвестной индуктивности L_x методом двух отсчётов
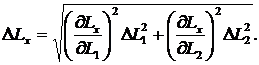    (19)
Вычисляя частные производные, и считая, что приборная погрешность одинакова для двух измерений , получим
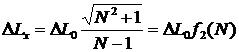.     (20)
Как видно из (20) с ростом коэффициента укорачивания погрешность измерения неизвестной индуктивности приближается к приборной погрешности. В табл. 2 приведены значения функции f₂(N) для разных коэффициентов укорачивания шлейфа N.

Таблица 2
Значения функции f₂(N) для разных коэффициентов укорачивания N

Для неизвестной индуктивности L_x существует ещё одна возможность её измерения методом двух отсчётов при использовании другого соотношения, в которое входит среднее значение двух приборных измерений:
. (21)
Из (21) видно, что погрешность измерения L_x, зависит от четырёх переменных. Общая формула для вычисления погрешности имеет вид
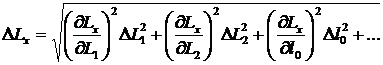.  (22)
Вычислим частные производные в (22)
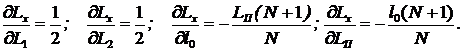(23)
Подставляя (23) в (22) и считая, что приборная погрешность одинакова для двух измерений, а погрешность измерения погонной индуктивности пренебрежимо мала по сравнению с приборной погрешностью, получим
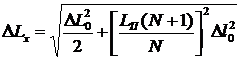.   (24)
Удовлетворительные измерения можно проводить в том случае, если слагаемые под радикалом (24) дают примерно одинаковые погрешности
.         (25)
В этом случае погрешность измерения неизвестной индуктивности совпадает с приборной погрешностью ΔL_x=ΔL₀.
Из равенства (25) можно оценить требуемую погрешность измерения ΔL₀ в зависимости от N и выбрать прибор, измеряющий начальную длину шлейфа
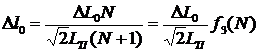.    (26)
Если в (26) подставить L_П=1 нГн/cм, а ΔL₀=0,01 нГн, то Δl₀ можно выразить в микрометрах
.  (27)
Зависимость погрешности Δl₀  от N представлена в таблице 3.

Таблица 3
Значения функции Δl₀  от N для разных коэффициентов укорачивания N

Из табл. 3 видно, что при N=2 погрешность измерения длины шлейфа Δl₀=47 мкм, а при N=5 – 59 мкм. Такая погрешность измерения длины требует привлечения штангенциркуля. Увеличение начальной базовой длины шлейфа l₀ до 5 см даст хорошие результаты.
Вычисление относительной погрешности по формуле (21) указывает на существенный недостаток рассмотренного способа:
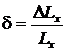.  (28)
Как видно из (28) и (21), относительная погрешность может быть достаточно большой за счёт возможной особенности знаменателя (28). Чтобы избежать этого, нужно положить
.   (29)
Тогда
.   (30)
С учётом значения погонной индуктивности значение L_x~1 нГн можно измерять при значениях начальной длины шлейфа, взятой в миллиметрах
.  (31)
При N=2 l₀=6,6 мм, а при N=5 – l₀=8,3 мм. Малое значение ΔL_x может быть обеспечено измерением длин шлейфа микрометром.

Выводы.

Предложен метод измерения погонной индуктивности и параметра среза магнитного поля, использующий в своей основе обработки результатов измерений линейную регрессию. Метод заключается в том, что к известной индуктивности L₀ подключаются одинаковые участки круглого проводника с одним диаметром, но различной длиной l₀. Наращивание индуктивности производят N раз по участку 2l₀.

Показано, что коэффициенты наилучшей прямой, лежащей в облаке экспериментальных точек, совпадают: один – со значением известной индуктивности, а другой – с погонной индуктивностью.
2. Предложен метод двух отчетов, применяемый для измерения индуктивностей порядка 1 нГн и меньше.
Он заключается в проведении двух измерений: первый раз измерение индуктивности проводится на длине шлейфаl0, а второй раз ─ на длине шлейфа, укороченной в N раз.
Получена формула для расчета погрешности неизвестной индуктивности, в которой подбором параметров удается добиться измерения неизвестной индуктивности с погрешностью прибора.
Показано, что требуемая погрешность измерения начальной длины шлейфа для N=2 и N=5 находится в диапазоне десятков микрометров. Ее удаётся уменьшить применением для измерения длины шлейфа микрометра.
Сделана оценка начальной длины шлейфа l₀, которая для N=2 и N=5 составляет значения 6,6 мм и 8,3 мм соответственно.

Работа выполнена по гранту РФФИ проект №12-08-00654-А.

Литература:

1. Tatiana Gaevskaya, Victor Karpovich, and Valentina Rodionova. High Q-Factor Wideband Resonators for Millimeter and Submillimeter Applications [Текст]: Hindawi Publishing Corporation. International Journal of Microwave Science and Technology. - Volume 2012 (2012), Article ID 842489, 3 pages, doi:10.1155/2012/842489, http://www.hindawi.com/journals/ijmst/2012/842489/
2. Kevni Büyüktas, Klaus Koller, Karl-Heinz Müller, and Angelika Geiselbrechtinger. A New Process for On-Chip Inductors with High Q-Factor Performance [Текст]: Hindawi Publishing Corporation. International Journal of Microwave Science and Technology. - Volume 2010 (2010), Article ID 517187, 9 pages, doi: 10.1155/2010/517187, http://www.hindawi.com/ journals/ijmst/2010/517187/
3. Patent WO 98/50956, International Patent Classification: H01L 29/00. Patterned ground shields for integrated circuit inductors [Текст]: Inventors: Yue C Patrick; Wong S Simon; Applicant: The Board of Trustees of the Leland Stanford Junior University. – Priority Data: 60/045,416, 02.05.97. – Pub. Date: 12 November 1998
4. А.С. Будяков, Е.М. Савченко, А.А. Пронин, П.А. Козынко СВЧ монолитная интегральная схема усилителя мощности на основе кремниевой технологии с выходной мощностью 1 Вт на частоте 800 Мгц [Текст]: Всероссийская научно-техническая конференция "Проблемы разработки перспективных микро- и наноэлектронных систем (МЭС-2010)". Сборник трудов /- М: 4-8 октябрь, 2010. – С. 577-582
5. Krutchinsky S., Prokopenko N. High-Frequency Sections of Active Filters of Mixed-Signal SoC Based on Current Amplifiers [Текст]: SRN Electronics, Volume 2012 (2012), Article ID 319896, 6 pages, doi:10.5402/2012/319896,  http://www.isrn.com/journals/electronics/2012/319896/
6. Крутчинский С.Г., Устинова Е.С., Будяков П.С., Прокопенко Н.Н. Высокочастотные полосовые RC фильтры на основе повторителей тока [Электронный ресурс] // Инженерный вестник Дона. 2012. №3, Режим доступа: http://www.ivdon.ru/magazine/archive/n3y2012/1035 (доступ свободный) – Загл. с экрана. – Яз. рус.
7. Крутчинский С.Г., Прокопенко Н.Н., Сухинин Б.М., Будяков П.С. Высокочастотные SiGe-избирательные усилители с узкой полосой пропускания [Электронный ресурс] // Инженерный вестник Дона. 2012. №3, Режим доступа: http://www.ivdon.ru/magazine/archive/n3y2012/1031 (доступ свободный) – Загл. с экрана. – Яз. рус.
8. Patent EP 1866937, Int Cl.: H01F 5/00, H01F 27/28, H01L 21/20, H01L 29/00. Integrated circuit transformer devices for on-chip millimeter-wave applications [Текст]: Inventors: Goren David [IL]; Pfeiffer Ullrich R [US]; Sheinman Benny [IL]; Shlafman Shlomo; Applicant: IBM [US]. – Priority: 08.04.2005 US 102292; Pub. Date: 21.11.2012
9. United States Patent Application 20030214378, Current U.S. Class: 336/200, International Class: H01F 005/00. Accurate multi-ground inductor for optical communication circuits [Текст]: Inventors: Tung, John C.; (Cupertino, CA); Zhang, Minghao (Mary); (Cupertino, CA); Assignee: Qantec Communication, Inc., Cupertino, CA. – Appl. No.: 10/146,854. – Filed: Mae 15, 2002. - Pub. Date: November 20, 2003
10. Сапогин В.Г., Прокопенко Н.Н., Марчук В.И., Манжула В.Г. Погонная индуктивность цилиндрических проводников с аксиальной плотностью тока в сложных функциональных блоках [Текст]: Инженерный вестник Дона. №4. Северо-Кавказский научный центр высшей школы Южного федерального университета. Ростов-на-Дону. 2012 г.